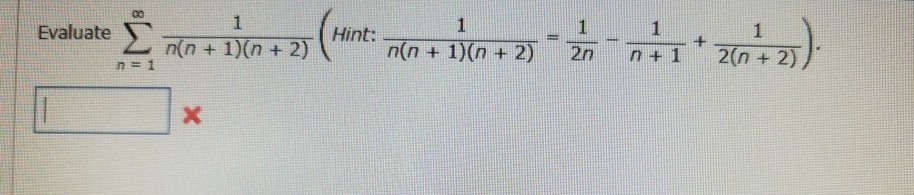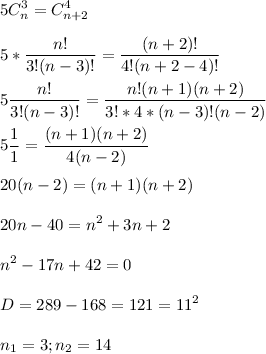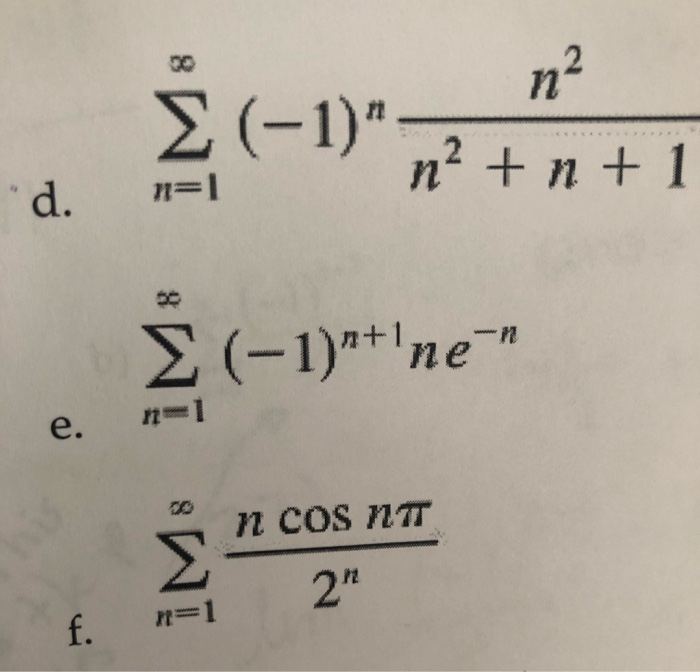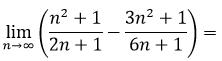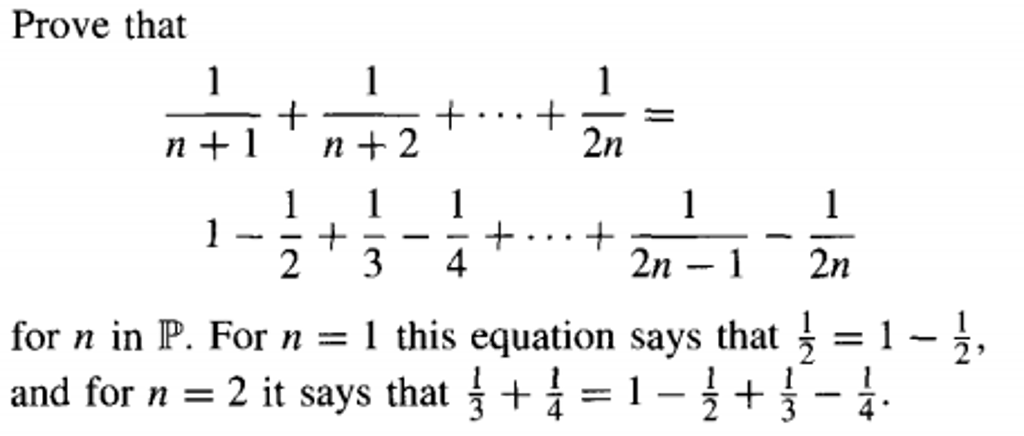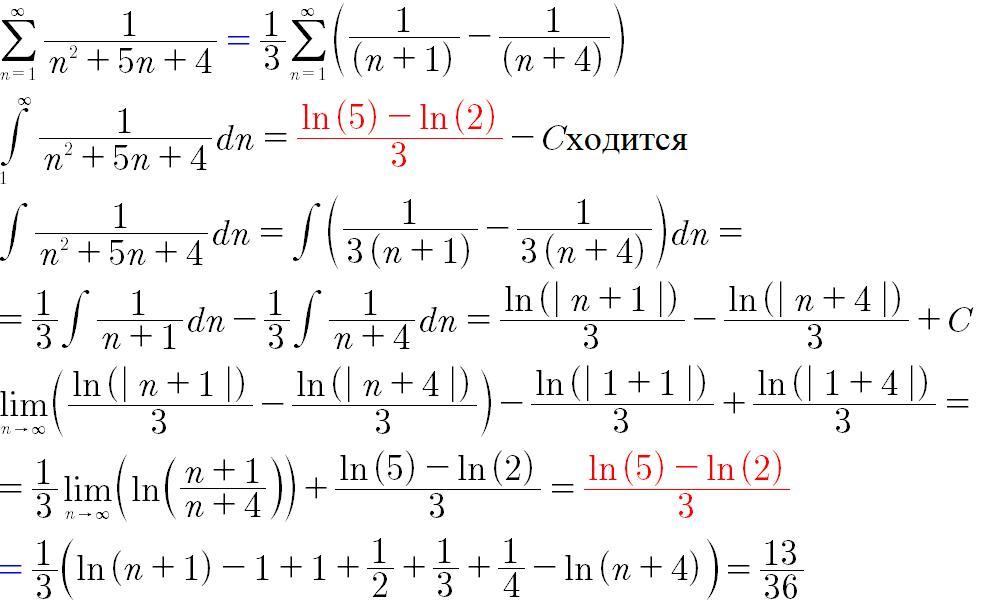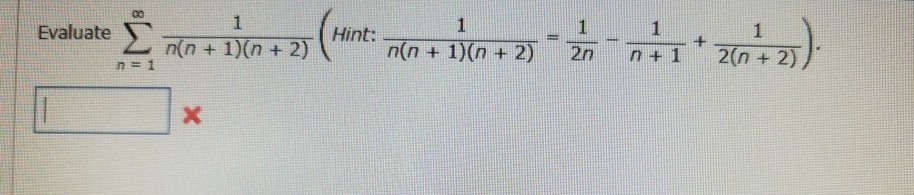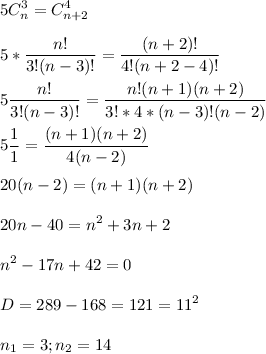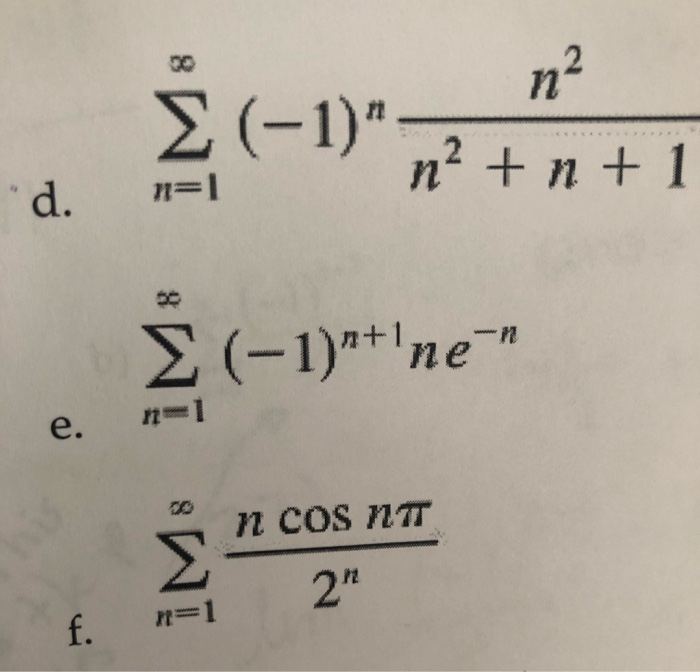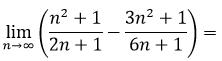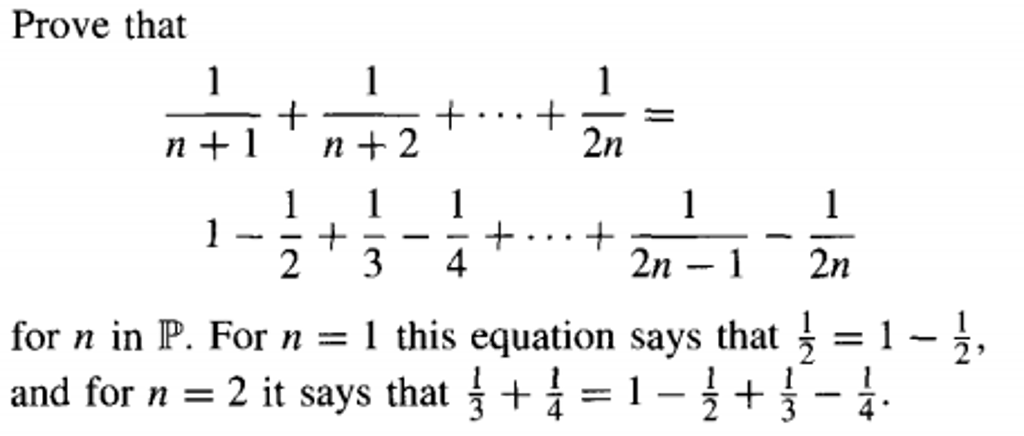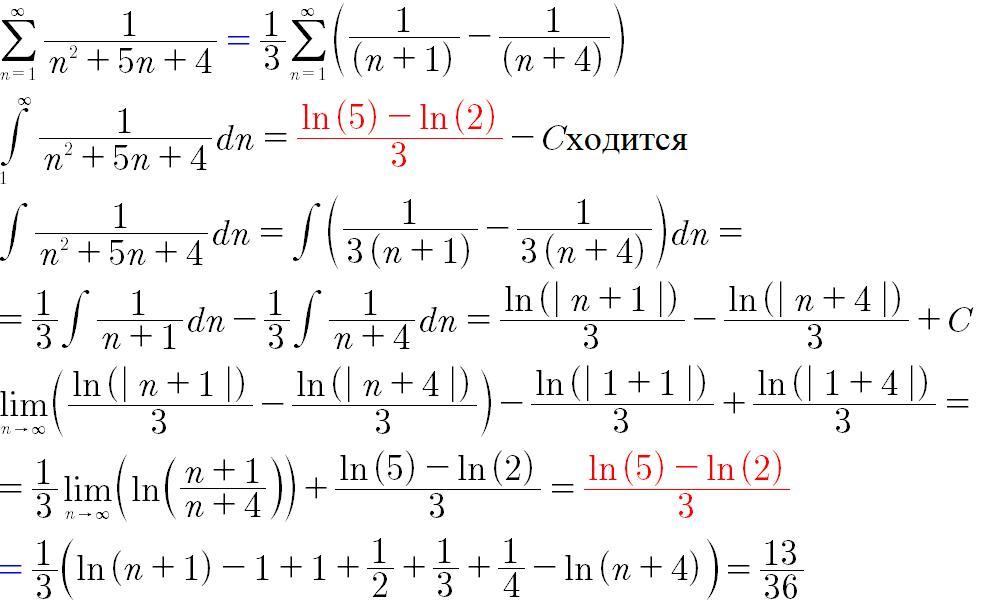1/2+1/3+1/4+ +1/n формула. +n/2^n=2-n+2/2^n формула. Сходимость ряда (-1)^n/(2n+1)^1/2. Г 1 2n 1 1 n. N(n-1)/2.
|
2n+2-2n-1+n2-1 общий знаменатель. N2 +(n+1)2 +. An=(3n-2)/(2n-1). Упростите выражение n!/(n+1). (2n-1)/2^n.
|
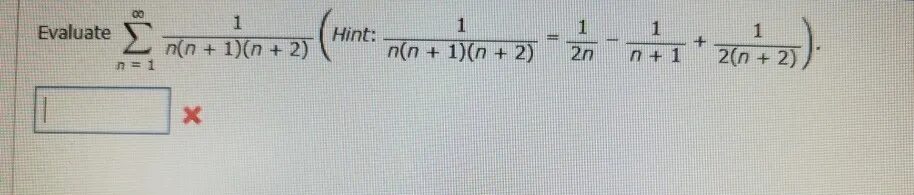Lim n стремится к бесконечности 3n+2/n+2. 1 3 2 5 n 2n+1 n 4n2 9n 5. С^5 n+3+c^4 n+3=c^5 n+4. Ряды n 2 4n 5 n2 2n 1. Lim(1+n)^2n.
|
Г 1 2n 1 1 n. Г 1 2n 1 1 n. Г 1 2n 1 1 n. Формулы метода математической индукции. (n+1)!/n!.
|
1^2+2^2+. Сходимость ряда 1/n 2. 1/2 + 3/2**2 +. Докажите неравенство 1/n+1 1/n+2. Г 1 2n 1 1 n.
|
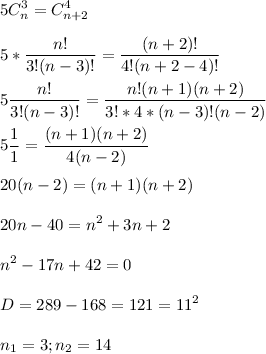(2n+1)(2n-1). (n-1)!+n!+(n+1)!=(n+1)²(n-1)!. 12 n 2 2n-3 3 n-1. Lim x стремится к бесконечности n^2+2n+5/2n^2. 1^3+2^3+.
|
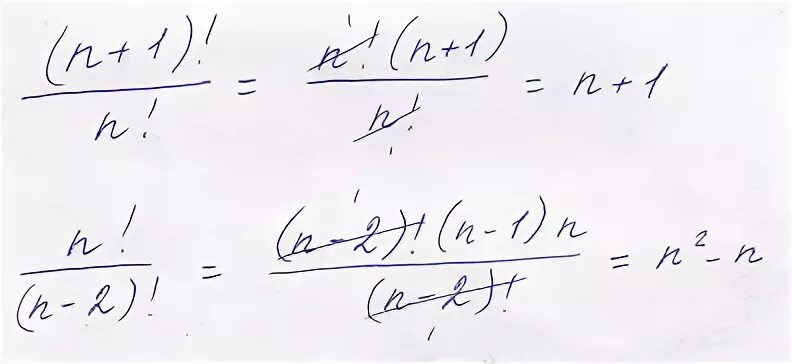Ряд 1/n^2. (2n+1)(2n-1). 1/n!-1/(n+1)!. ∑_(n=1)^∞(n/(2n+1) )^(n ) 〗. 2n+1/(n+1)^2*(n+2)^2.
|
Limn2n2n2n2. Формула 2n-1. Г 1 2n 1 1 n. 1/2+2/2^2+. +n^3.
|
Г 1 2n 1 1 n. Решите уравнение c/c+3=c^2/c+3. 2n 2n 2n. N+3/2n-n+1/2n+2+3/n-1. (2n+1)(2n-1).
|
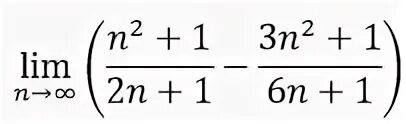(n^2+1)^2. Г 1 2n 1 1 n. Доказать методом математической индукции 1*2+2*5+3n2. Доказать что 2^n>2n+1. Ряд (2n-1)!!/n!.
|
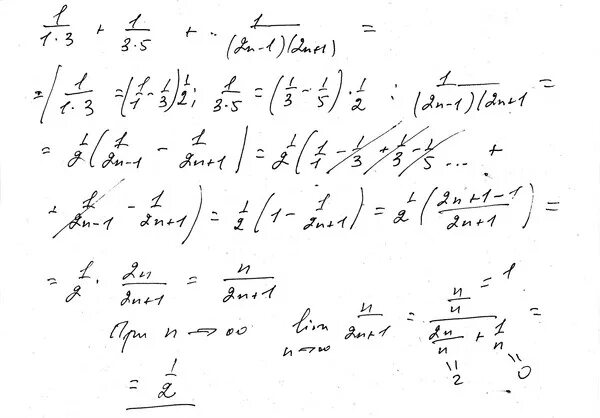Интеграл xsinx. Решите уравнение: n!/(3!(n-3)!)=(n+2)!/(1/5)(4!(n+2-4)!). 2n+1/(n+1)^2*(n+2)^2 исследовать числовой ряд. + 2n-1 // 2 ** n. ((n!)^2)/(2^n^2).
|
Г 1 2n 1 1 n. 5n+1-5n-1/2 5n. Г 1 2n 1 1 n. (n+2/n+1) * (1-1/(n+1)^2)^n. Докажите неравенство 1 n 1 1 n 2 1 2n 13 24.
|
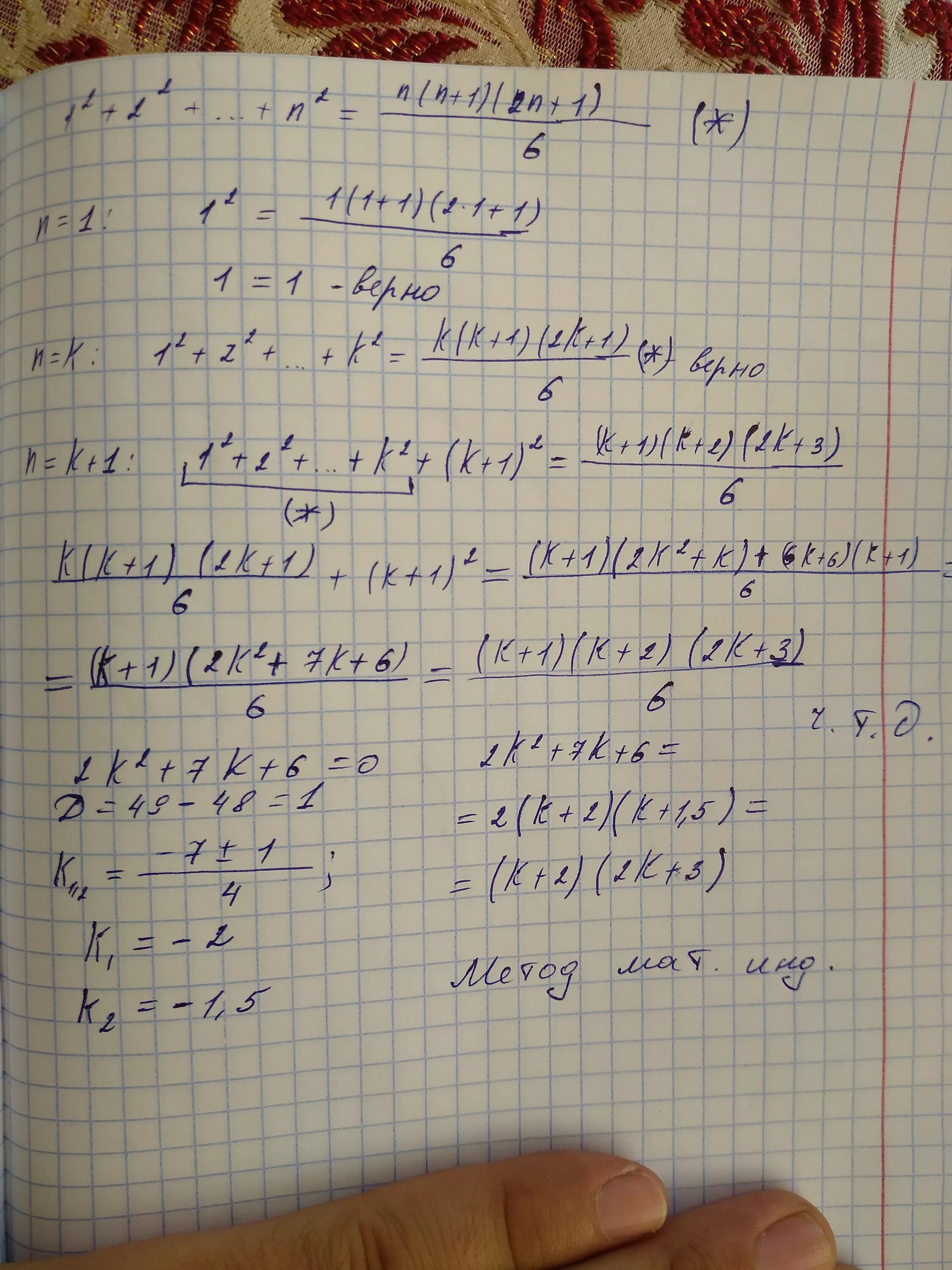Интеграл x 2 sqrt 1-x 2. ((n!)^2)/(2^n^2). Предел (n+1)^2/2n^2. Сократи дробь n2+n n2+2n. 5 2/3-4 решение.
|
Lim(5-2^-n). Сходимость ряда (-1)^n * 4^n / (n+1)!. N1a1. Интеграл sqrt(1-x^2). Г 1 2n 1 1 n.
|
Г 1 2n 1 1 n. Доказать методом математической индукции. 1/2+1/3+1/4+ +1/n формула. + (2n)2. (n+1)^3 формула.
|
N n-1 упростить. N n2 n3. Г 1 2n 1 1 n. Г 1 2n 1 1 n. +n^2.
|
Г 1 2n 1 1 n. Ряд 2n-1/2^n. N+3/2n+2-n+1/2n-2+3/n2-1. Г 1 2n 1 1 n. 2+7+14+ n 2+2n-1.
|
Предел последовательности n+2/2n+1. Г 1 2n 1 1 n. Г 1 2n 1 1 n. Г 1 2n 1 1 n. U_{n}=(2n-1)/(n^2+n-1).
|
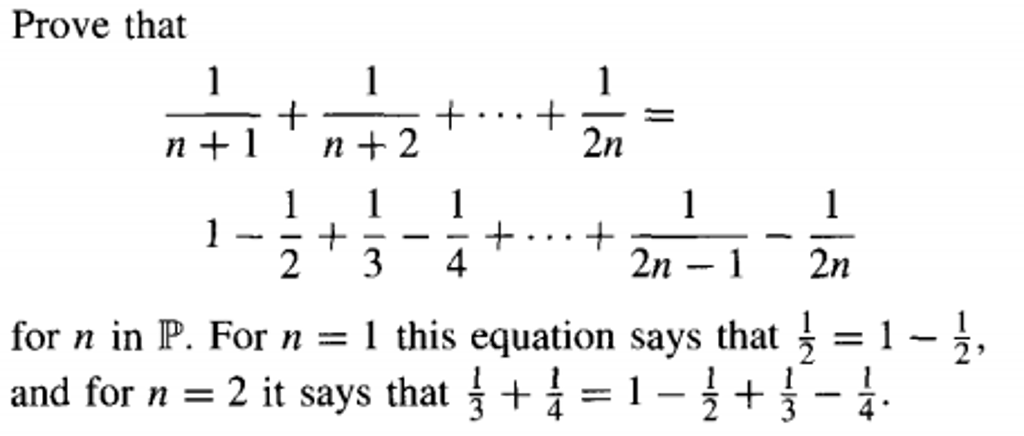Г 1 2n 1 1 n. (2n-1)/2^n. Интеграл sinx. (n+1)!/n!. Ряд 1/n^2.
|
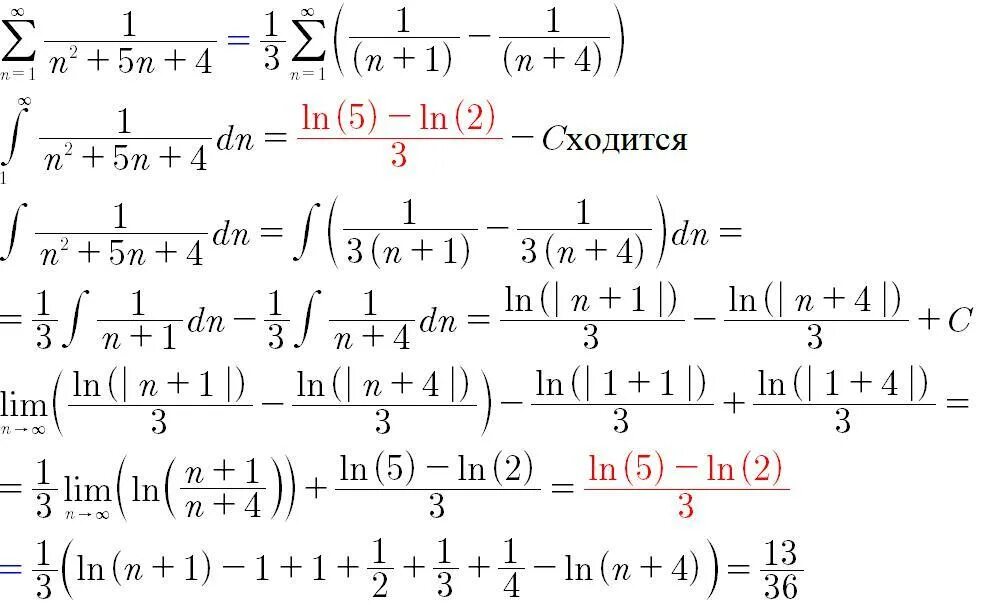Lim n стремится к бесконечности 3n+2/n+2. N n2 n3. Г 1 2n 1 1 n. Lim(1+n)^2n. An=(3n-2)/(2n-1).
|
